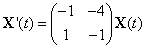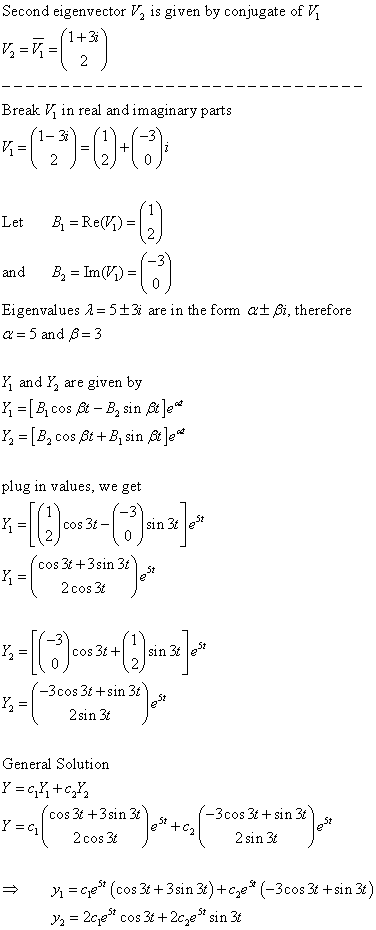Sunday, February 18, 2018
Solve the following differential equation using Laplace Transforms. y'' + y' - 2y = -4 , y(0) = 0 , y'(0) = 0
Solve the following differential Equation using undetermined coefficients. y'' - 15y' + 57y = 9e^(8t)
Saturday, February 17, 2018
Solve differential equation using Laplace Transforms. y'' - 6y' + 5y = te^t , y(0) = 2 , y'(0) = -1
Solve by using Laplace Transforms. y'''' - 9y = 0 , y(0) = 1, y'(0) = 0 , y''(0) = 0 , y'''(0) = 1
Question. Solve by using Laplace Transforms.
y'''' - 9y = 0 , y(0) = 1, y'(0) = 0 , y''(0) = 0 , y'''(0) = 1
Solution:

y'''' - 9y = 0 , y(0) = 1, y'(0) = 0 , y''(0) = 0 , y'''(0) = 1
Solution:

Thursday, February 15, 2018
Write the form of particular Solution with the method of undetermined coefficients.
Thursday, January 18, 2018
Find the general solution of the following equation. y'' - 4y' + 4y = (e^2x)/x
Find the inverse Laplace transform 6/(s^3+3s)
Subscribe to:
Posts (Atom)