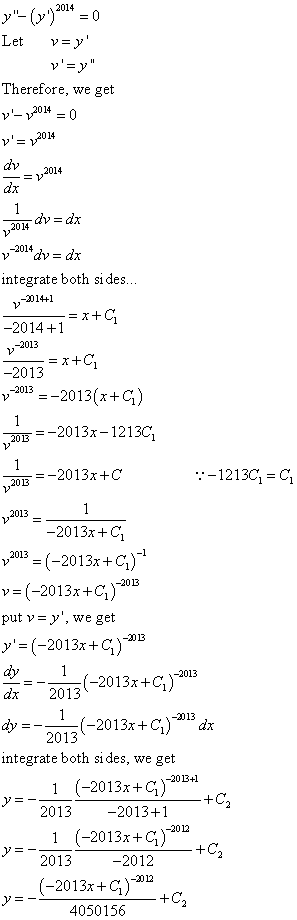Sunday, October 29, 2017
Friday, October 27, 2017
Solve the following differential equation using annihilator method y'' + 3y' -2y = e^(5t) + e^t
Wednesday, October 25, 2017
Solve the differential equation. y’’ –(y’)^2014 = 0
Solve the IVP. y’ – (1/t)y = e^t y^2 , y(1) = 305
Solve the exact differential equation. (e^y + x^2 + sin(y)) dx + x(e^y + cos(y)) dy = 0
Monday, October 23, 2017
Use Euler's method to obtain a four-decimal approximation of the indicated value. Use h = 0.5 ; y' = 3x^2/2y , y(0) = 1, y(2)
Solve the system of differential equations by systematic elimination. dx/dt = -2x - y ; dy/dt = -4y
Use Euler's method to obtain a four-decimal approximation of the indicated value. use h = 0.5 y' = 3x^2/2y ; y(0) = 1 ; y = 2
Solve the following Cauchy-Euler equation x^2y'' + 5xy' - 5y = 0
Solve the IVP (2xy + x^4)dx + (x^2 + y^2)dy =0 y(0)=1
Solve the IVP. dy/dt - 2ty = -6t^2 e^(t^2) ; y(0) = 1
Find the differential equation that has y^2 = Cx + 3 as its general solution
Find inverse Laplace transform of e^(-2s)/( s^2(s-1) )
Saturday, October 21, 2017
Use Euler’s method with h = 0.1 and h = 0.05 to calculate y(1.2) ; dy/dx = 2x – 3y + 1 , y(1) = 5
Find the Laplace Transform of f(t) = {cos t , 0 <= t <= Pi ; 0, t >= Pi} using definition of Laplace Transform.
Friday, October 20, 2017
Solve the initial value problem. y’’ – 5y’ + 6y = 0 , y(0) = 3 , y’(0) = 5
Use Euler's Method to compute y(4) given that y' = y - x^2 , y(1)
Solve the differential equation dP/dt = kP - C
Solve the separable differential equation dy/dx = -0.8/cos(y) with initial condition y(0) = pi/4
Solve the separable differential equation y’ = sqrt(-2y + 41) with initial condition y(-5) = 8
Use Euler’s method to calculate y(0.5) using h = 0.05 and h = 0.1 y’ = e^(-y) , y(0) =0
Use Euler’s method with step size 0.5 to compute the approximate y-values y(1.5), y(2), y(2.5) and y(3)
Solve the following exact differential equation. ( 6xye^(2y) + 4x^3 ) dx + ( 3x^2 e^(2y) + 6x^2 ye^(2y) - 2sin(2y) ) dy = 0
Question.
Solution:
Solve the following exact differential equation.
( 6xye2y + 4x3 ) dx + ( 3x2e2y + 6x2ye2y - 2sin(2y) ) dy = 0
Solution:
dy/dx = (1+y^2)/(y+yx^2)
Determine the general solution of the first order differential equation: dy/dx = 2y ln y + xye^(2x)cos(3x) , y>0
Thursday, October 19, 2017
Solve the IVP xy'-2y=x^2+6 , with y(1)=1 by method of variation of parameters
Wednesday, October 18, 2017
Use Euler's method to obtain a four-decimal approximation of the indicated value. y' = 2x - 3y + 1, y(1) = 3; y(1.2)
Subscribe to:
Posts (Atom)