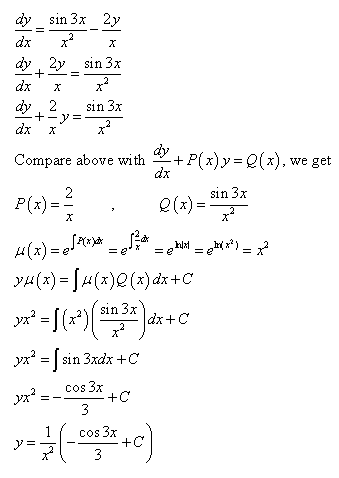Sunday, August 9, 2015
laplace transform of the piecewise function y' -3y = {3, 0<= t< 1; 0, 1<=t}, y(0) = 2
inverse laplace transform of (9s-3) / ((s-3)^2 +9)
inverse laplace transform of (3s-15) / (s^2 - 8s + 20)
y'' +4y = {4, 0 <= t< 1; 0, 1 <= t} y(0) = 3 y'(0)= -2
x' = -6x - 4y , y' = -3x - 10y
Friday, August 7, 2015
x' = y - x + t , y' = y , x(0)=6 , y(0)=8
y''''-9y=0 , y(0)=1, y'(0)=0, y''(0)=0, y'''(0)=1
y''-6y'+5y=te^t y(0)=2, y'(0)=-1
dy/dx = 3e^(2x) , y(0) = 5/2
dy/dx = 3x^2 y^2 - y^2
Find the general solution to the differential equation
dy/dx = 3x^2 y^2 - y^2
Find the particular solution for which y(0) = 1 ie when x = 0 , y =1

dy/dx = 3x^2 y^2 - y^2
Find the particular solution for which y(0) = 1 ie when x = 0 , y =1

y'' + 8y' + 25y = 0 , y(0) = 1 , y'(0) = 8
Wednesday, August 5, 2015
Particular Solution of 3y'' + y' + 2y= 5t + 2
Tuesday, August 4, 2015
Inverse Laplace Transform s^2/(s+1)^3
y'' + 2y' + 24y = 8cos(4x)
dy/dx = 1/(x^2 - 3x) , y(4) = (2/3) ln(4)
dy/dx = (-2x^3 - 2y)/(6x - y^4)
y'' - 2y' = e^t/(t^2 + 1)
dy/dx= xy + 7x +2y + 14
Fundamental set of solutions (Wronskian)
Inverse Laplace Transform of 1/(s^2 - 8s + 17)
Subscribe to:
Posts (Atom)